• String to List
• List to String
• Addition
• Carries
• Multiplication
• Exponentiation
• Factorial
• Subtraction
• Division
• Euclidean Algorithm for Greatest Common Factor

      The TI-85 has a "word size" for its real number type:  14 digits, of which only 12 are shown.  On this page we see how to use strings and lists to get around this limitation.

The key to following program converts a string of digits to a list of real numbers:
Program ST2L

:ClLCD
:Disp "Inpt strng of digits"
:InpSt ST    // Each character in the string is a numeral
:lngth ST->dimL NL  // Dimension a list, NL, of the same length as ST
:For(I,1,lngth ST)
:  sub(ST,I,1)->P // Extract the Ith character in ST to P
:  St>Eq (P,G)   // Convert the character P to an expression G
:  G->NL(I) // Store the expression G as the Ith real in list NL
:End

     How does the above algorithm work?  Well, after prompting the user to input a string, the For loop steps through the characters in the string (ST) and converts each into an equation. This may seem a startling type-cast at first, but it's purpose is clear when you consider that it allows character "3" (considered a string on the '85) to become the equation 3, which automatically becomes a real number after it's transferred to the list.  When it's done, we have a list of digits!

Going Backwards: Converting a List to String

     Consider the list of digits to represent an array of coefficients of powers of 10:
[4 5 4 0 9] = 4*10⁴ + 5*10³ + 4*10² + 9 = 45,409
- just like regular, every day place value numbers.  The bonus here is that, while the '85 routinely works only with 14 digit numbers (of which it shows 12). By contrast, a list may contain thousands of digits - it is restricted only by the memory available.

      So far we have a way of entering in a number with more than 14 digits.  Assuming we have procedures for operating on these, we'll then need some way to output the result. The following algorithm makes use of the way the "+" is overloaded on the '85 so that strings can be concatenated.

Program L2ST

:" "->ST2  // Create and initialize string
:1->B
:While C(B)==0   // Skip over leading zeroes.
:  B+1->B
:End
:For (I,1,dimL C)  // From 1st non-zero element to end of C
:  If C(I)==1        // Handle each digit case separately:
:  ST2+"1"->ST2
:  If C(I)==2
:  ST2+"2"->ST2
:  If C(I)==3
:  ST2+"3"->ST2
:  If C(I)==4
:  ST2+"4"->ST2
:  If C(I)==5
:  ST2+"5"->ST2
:  If C(I)==6
:  ST2+"6"->ST2
:  If C(I)==7
:  ST2+"7"->ST2
:  If C(I)==8
:  ST2+"8"->ST2
:  If C(I)==9
:  ST2+"9"->ST2
:  If C(I)==0
:  ST2+"0"->ST2
:End // End the For loop
:sub(ST2,2,lngth ST2-1)  // Print the number string

     The While loop in the beginning serves to advance the current position in the list (C) to the first non-zero number before starting the conversion to a string (ST2).  This is done simply because leasing zeroes add no value to a number. That is, for example, 00123 =123.

Addition

     Ok, we know how to get large numbers in and out of the calculator. How do we perform operations on the lists?

     Consider addition first. If we want to add [1 3 1 2 4 1] and [2 7 3 2 1 2], (131241+273212) and get 404453, we only have to add the lists and, if a number is >10, carry the overflow to the next number. Using "+" to add the lists, we wind up with

We want to "carry" this number to [4 0 4 4 5 3].  Keep in mind that the lists simply represent coefficients of (10^N).  If one of its coefficients is >10 (say 10a+b), then this number actually represents  a*10^(N+1) + b*10^N.

   

---

     The algorithm for converting a number of the form  a*10^(N+1) + b*10^N.where the coefficients may be integers larger than 9 to an equivalent expression in which all the coefficients (place values) are numerals.  The algorithm simply goes from the end of the list (1's place) to the front, carrying the appropriate excess to the next list position.
Program Carry

:For(I,dimL C,2,(-)1)
:(C(I)-mod(C(I),10))/10+C(I-1)->C(I-1)
:mod(C(I),10)->C(I)
:End

     The mod(C(I),10) command gets the least significant digit (the units digit.)  Subtracting this from the number and then dividing the number by 10 effectively shifts the number one digit to the right - giving you the number that you want to add (carry) to the next highest power position. mod(C(I),10)->C(I) serves to leave the units digit behind where it belongs.

     Load  [3 10 4 4 5 3]  into C and run Carry.  Everything's great, huh?  Except for two little problems:

1. What if we need to carry from the most significant place value? You can't just     redimension the same list to have one more digit, since the new position would
    be on the wrong end of the list.
2. What if the two numbers don't have the same number of digits?
     To get around both of thes problems, we can invent a list for the sum that has one more digit than the list with the most elements. For example, if we're adding 8123 and 1221132, we'd dimension a new list with 8 elements.

     First work out the special case when both numbers have the same number of digits -- say, n. Dimension a list C with n+1 elements to hold the sum and add i-th elements of addend lists to the i+1-st position in C. This leaves room for a carry in the first position, if it's needed. For example, with addend lists: [8 3 2 4 2] and [3 2 1 4 5], we'd end up with
C=[0 11 5 3 8 7] which becomes [1 1 5 3 8 7] after a carry and then 115387 after a list to string operation.

    For the more complicated situation where one addend has more digits than the other, irst dimension a list of seven elements. After this we'd add put the second number in the last six positions to have [ 0 3 2 1 4 5 7] and then add the first number to the final positions, to get [0 3 3 4 2 9 9].  All we have to do is check for carries and perform them, if necessary and we have our result. This is the principle used in the following source code:

:ClLCD
:0->C       // Clear C.
:Disp "ADDITION"
:Disp ""
:InpST ST
:ST2L       // Convert the string to a list.
:NL->AB    // Save the first addend in AB
:InpST ST
:ST2L
:NL->AC   // Save the second addend in AC
:1+max(dimL AB,dimL AC)->dimL C
       //  dimension C as 1 larger than the largest of AB and AC.
:If dimL AB>dimL AC
:Then
:  AC->LL  // Be sure the larger number is AC - memory?!
:  AB->AC
:  LL->AB
:  ""->LL
:End
:If dimL AB==dimL AC  // AB and AC have the same number of digits.
:Then
:  For(P,2,dimL C)
:    AB(P-1)+AC(P-1)->C(P) // Leave C(1) open for a carry.
:  End
:Else // Here we know AC has more digits.
:  For(P,2,dimL C)
:    AC(P-1)->C(P) //Copy the larger number to C leaving C(1) open.
:  End
:  For(P,dimL C-dimL AB+1,dimL C,1) // Starting from the most
:    C(P)+AB(P-dimL C+dimL AB)->C(P) // significant digit of
:  End // the smaller addend, add them into the corresponding position of C
:End
:Carry // Apply the carry program to C
:L2ST // Print the result.

Multiplication

     Suppose we want to compute 3490529510847650949147849619903898133417764638493387843990820577 * 32769132993266709549961988190834461413177642967992942539798288533?

     Most humans are understandably reluctant to perform this computation by hand. When multiplied out they produce a famous number, RSA-129: so named because it was part of an RSA challenge.  (Mark Janeba has an excellent article on the factorization of RSA-129, if you're interested.)  The challenged issued was to factor the 129 digit number:

114381625757888867669235779976146612010218~
   296721242362562561842935706935245733897830~
      597123563958705058989075147599290026879543541
    It's been estimated that, using 1977  technology, it would take about 40 quadrillion years to factor this number!   Fortunately, multiplying the factors (even by hand) does not take nearly so long.  Is the TI-85 is up to the task?

     Representing the two factors as 64 and 65 digit lists, we have:

(34905...77)*(32769...33) = (3*10⁶³+4*10⁶²+^...+7)*(3*10⁶⁴+2*10⁶³+^...+3)       = (3*3)*10¹²⁷+(3*2+4*3)*10¹²⁶+^...+21

     Ignoring the need to carry, the algorithm to we want to find these coefficients is just the algorithm for finding the coefficients of a product of polynomials.  Then we can apply a Carry algorithm to finish.

     The formula for the kth coefficient is  sum(a_i*b_j,such that i+j=k).  Where  a_i is the i+1 digit in A and  b_j is the j+1 coefficient in B.  Note that this syntax doesn't correspond to the sum syntax on the '85. No bother, just compute all possible products of coefficients, choosing a digit factor from each using nested For loops and add them to a running total of the appropriate coefficient sum.  Look closely at the nested For loops below and try a few examples by hand to see how they work.

Program =MULT

:0->C  //Clear out C
:ClLCD
:Disp "Long Integer"
:Disp "Multiplication"
:Disp ""
:InpST ST
:ST2L
:NL->A  // Input first factor to list A
:InpST ST
:ST2L
:NL->B // Input second factor to list B
:dimL A+dimL B->dimL C // The digits in product is sum of factor's digits.
:For(I,1,dimL A)
:  For(J,1,dimL B)              // Each product is computed once
:    C(I+J)+A(I)*B(J)->C(I+J)  // and added to proper coefficient.
:  End
:End
:Carry
:L2ST

Exponentiation

     Can we use these techniques to compute B^N ?  How about the factorial of B, B! ?  Each of these is reduceable to repeated multiplication.  That is, B^N = B*B*...*B   is  N  factors of  B.   Similarly  B! =  B*( B-1)*( B-2)*...*3*2 has  B  factors each 1  smaller than the previous.

     To exponentiate a positive integer B to an integral exponent, N, we could apply the multiplication algorithm described above N-1 times, and dimension the product to the appropriate size, but this assumes that B and N may need to be more than 14 digits.  Now, the number of digits in B^N  is 1 + log(B^N) = 1 + N*logB - which can be a very large number, especially if the exponent is large. This can easily produce lists which are outside of the calculator's memory capacity.  2^123456789123456 will have trillions of digits!  Even if the exponent and base are modest, there is a memory and time problem. For 125^99, the list will contain  1+iPart 99*log125=208  digits, occupying  2087  bytes in memory - a problem if you've got a lot of stuff in memory already.  999^99 is 297 digits which requires 2977 bytes in memory. It takes an eternity to compute and quite a while just to scroll throught the numbers on the screen.

      Thus, we can safely assume that both B and N are ordinary TI reals with less than 15 digits.  It's then a simple matter to dimension the list for the B^N number using 1+iPart(N*logB)->dimL C, load it initially with B->C(dimL C) and then start the multiply and carry loop:

Program POWER

:ClLCD
:0->C // Initialize C
:Disp "Compute B^N"
:Disp ""
:Input B  // A is the base of the exponential.
:Input N  // B is the exponent.
:iPart (N*log N)+1->dimL C //Note that 1+log(A^B) gives decimal digits.
:B->C(dimL C)  // The (dimL C) is needed to keep the list type.
:For(I,1,N-1) // Multiply A (already in C) by A, B-1 times.
: If max(C)*A>2E13 // If the largest number in C*A is greater than 2*10¹³
: Then    // mult by A may get a list element with more than 14 digits,
:  Carry // so get a list of digits with equivalent value.
: End
: C*B->C
:End // End For loop.
:CARRY
:L2ST

     To see how this works, try walking through and example.  In 1883, Pervouchine showed 2⁶¹-1  is prime.  Let's see if we can figure out what it is.  It's got  1+iPart(61*log2)=19 digits.  The algorithm loads 2 as the 19th element in the list. Here is a snapshot of the list after each for cycle:

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8]
. . . Keep multiplying by 2 until 2*2⁴⁴ > 2*10¹³
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 17592186044416]
. . . then do a CARRY
[0 0 0 0 0 1 7 5 9 2 1 8 6 0 4 4 4 1 6]
. . . and multiply by 2 some more:
[0 0 0 0 0 2 14 10 18 4 2 16 12 0 8 8 8 2 12]
[0 0 0 0 0 4 28 20 36 8 4 32 24 0 16 16 16 5 24]
[0 0 0 0 0 8 56 40 72 13 8 64 48 0 32 32 32 10 48]
. . . 9*2¹⁶ does not exceed 2*10¹³ so at the last multiplication
the list is 9*2¹⁶ = 65536*[0 0 0 0 0 1 7 5 9 2 1 8 6 0 4 4 4 1 6]
= [0 0 0 0 0 65536 458752 327680 589824 . . . 393216]
. . . which after a CARRY becomes
[2 3 0 5 8 4 3 0 0 9 2 1 3 6 9 3 9 5 2]
. . . and after the final L2ST, 2305843009213693952: the number 1 more than the 9th Mersenne prime: 2⁶¹-1.

      The TI-85 handles the next 3 Mersenne primes easily:  2⁸⁹-1, 2¹⁰⁷-1, 2¹²⁷-1.
In 1952, Robinson discovered the next 5 Mersenne primes:  2⁵²¹-1, 2⁶⁰⁷-1, 2¹²⁷⁹-1, ²²⁰³-1 and 2²²⁸¹-1. How does the '85 do with these?

Why wait until the list elements are large to do the carry?

---

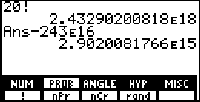
       You can use the built-in factorial routine ([2nd] [x] [F2] [F1]) to compute factorials, but starting with 20! we loose precision. As the screen shot shows, we can get 13 accurate digits by subtracting off the leading digits, but the 14th is suspect since the 15th digit is missing and there may have been some round off.

      Using the list type to compute larger factorials is quite simple, though you may wonder how we can compute log(N!), in the process of computing N!.  There are two good reasons making this possible. One is that we don't need an exact value for log(N!) since we end up just taking its integer part, and the second is that log(N!) = sum(logk, k, 2, N).

FCTRL Program

:0->C
:ClLCD
:Disp "N FACTORIAL"
:Disp ""
:Input N // N is an integer less than 14 decimal digits.
:iPart (log (N!))+1->dimL C // Formula for number of decimal digits.
:N->C(dimL C) // Enter N as the last entry in list C.
:For(K,N-1,2,-1) // Be sure to enter [(-)] for negative
:  C*K->C
:  If max(C)*K>2E13
:  Then
:    CARRY
:  End
:End
:CARRY
:L2ST

Subtraction

Here's a routine to do subtraction of large integers.

:ClLCD
:0->C
:Disp "SUBTRACTION"
:Disp ""
:InpST ST
:ST2L           // Get AB and AC to subtract AC from AB
:NL->AB
:InpST ST
:ST2L
:NL->AC
:dimL AB->dimL C // Create C to hold the difference
:For(P,dimL AB,dimL AB-dimL AC+1,-1) // Start at the right end
: If AB(P)>=AC(P-dimL AB + dimL AC)  // Check to see if you need to borrow
: Then
:  AB(P)-AC(P-dimL AB+dimL AC)->C(P)
: Else // Borrow
:  1->K
:  While AB(P-K)==0 // Look for the first non-zero value to borrow from.
:   9->AB(P-K)
:   K+1->K
:  End
:  AB(P-K)-1->AB(P-K)
:  AB(P)-AC(P-dimL AB+dimL AC)+10->C(P)
: End
:End
:For(P,dimL AB-dimL AC,1,-1)
: AB(P)->C(P) // Copy the rest of the digits we won't subtract from.
:End
:L2ST

Division

     So you want to implement the division algorithm to produce a quotient and a remainder when two large integers (AB/AC) are divided?  This is a bit longer than the others and required using more of the design process - though I imagine someone could reduce the code length here with a little ingenuity.

     The key elements of the subtraction routine above0 are used to do repeated subtraction with borrowing. There are tests to see if subtraction is required and then an index, I, keeps track of how many times the divisor is subtracted in a specific place value, P, which is in the list of quotient digits, C.  When all that can be subtracted is taken out, I is the numeral written to that place value in the quotient.  When the procedure is finished, the remainder is in AB.

:ClLCD
:0->C
:Disp "DIVISION"
:Disp ""
:InpST ST
:ST2L
:1+dimL(NL)->dimL AB  //Make room for a leading 0 in dividend
:0->AB(1)
:For (N,1,dimL NL)
: NL(N)->AB(N+1)
:End
:InpST ST
:ST2L
:NL->AC   //AC is the divisor.
:dimL AB-dimL AC->dimL C
:1->P   // "P" will index the place value.
:Lbl Loop
: 0->I  // "I" will count how many times we subtract for given place value, P.
: 1->J  // J is used to step through digits to check is subtraction is needed.
: If AB(P)>0 // If the current remainder has place value > divisor.
: Then
:  SBTR   // Execute subtraction subroutine.
:  Goto HOP
: End
: 1->next
: while next        // Check to see if subtraction is called for.
:  If AC(J)<AB(P+J)
:  Then
:   0->next  // Exit while loop.
:   SBTR   // Execute subtraction subroutine.
:   Goto HOP
:  Else
:   If AC(J)>AB(P+J)
:    0->next  // Exit while loop without subtracting.
:  End
:  Lbl HOP
:  Disp "AB",AB  // Debugging.
:  Pause
:  J+1->J    //Compare next digits.
:  If J>dimL AC  // In this case, all the digits are equal.
:  Then
:   0->next     // Special case where digits are equal,
:   For(M,1,dimL AC) // subtraction will leave all 0's.
:    0->AB(P+M)
:   End  // End For.
:  End  // End If.
: End  // End While.
: Disp "I = ", I  // Debugging.
: I->C(P)   // Write quotient digit to list.
: P+1->P   // Advance to next place value.
: If P<dimL C+1 // If there are more digits to compute,
: Goto Loop    // go compute them.
:L2ST   // Show quotient
:Disp "The remainder is = ",AB  // Show remainder.
SBTR
:While 1      // Keep looping until a "return" is encountered.
: Disp "SUB"  // Debugging.
: 1->K
: 1->fk
: while fk     // While more subtraction neede for this place value.
:  If AB(P)>0  // Don't wait for need to borrow,
:  Then       // just dump this place value in the leading
:   0->fk    // digit corresponding to leading digit in AC.
:   10*AB(P)+AB(P+1)->AB(P+1)
:   0->AB(P)
:  End
:  If AC(K)<AB(P+K)
:  Then
:   0->fk  // Exit While check and commence with subtraction.
:  Else
:   If AC(K)>AB(P+K)
:    Return  // Can't subtract - move on to next place value.
:  End
:  K+1->K // K only increases only if digits in AC match those in AB.
: End
: If K==dimL AC+1
: Then
:  For(M,1,dimL AC)  // If digits in AB are the same as those in AC,
:   0->AB(P+M)      // The differeces will all be zero.
:  End
:  Return
: End
: For(G,dimL AC,1,-1)
:  If AB(P+G)>=AC(G)
:  Then
:   AB(P+G)-AC(G)->AB(P+G)
:  Else
:   AB(P+G)-AC(G)+10->AB(P+G)
:   1->M
:   While AB(P+G-M)==0
:    9->AB(P+G-M)
:    M+1->M
:   End
:   AB(P+G-M)-1->AB(P+G-M)
:  End
: End
: I+1->I
:End