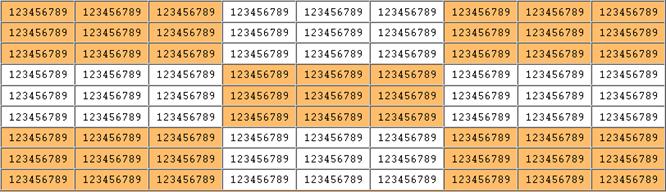
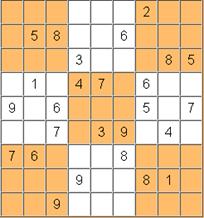
|
|
1 34 6 |
34 7 9 |
1 34 |
1 5 78 |
1 45 89 |
1 45 7 |
2 |
3 67 9 |
1 34 6 9 |
|
1234 |
5 |
8 |
12 7 |
12 4 9 |
6 |
1 34 7 9 |
3 7 9 |
1 34 9 |
|
12 4 6 |
2 4 7 9 |
12 4 |
3 |
12 4 9 |
12 4 7 |
1 4 7 9 |
8 |
5 |
|
23 |
1 |
23 |
4 |
7 |
2 5 |
6 |
23 9 |
23 89 |
|
9 |
234 8 |
6 |
12 8 |
12 8 |
12 |
5 |
23 |
7 |
|
2 5 8 |
2 8 |
7 |
12 56 8 |
3 |
9 |
1 |
4 |
12 8 |
|
7 |
6 |
12345 |
12 5 |
12 45 |
8 |
34 9 |
23 5 9 |
234 9 |
|
2345 |
234 |
2345 |
9 |
2 456 |
2345 7 |
8 |
1 |
234 6 |
|
12345 8 |
234 8 |
9 |
12 567 |
12 456 |
12345 7 |
34 7 |
23 567 |
234 6 |
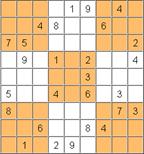
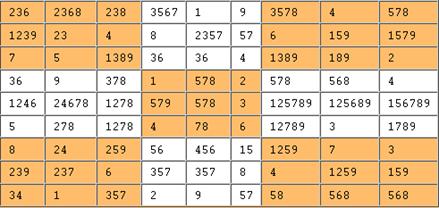
We can immediately conclude that (6,7) = 1. The singletons are few, now. The entries (5,2) = 4 and (6,1) = 5 are singletons in their block. This causes the singleton (5,8) = 3 in the 5th row.
Also, (8,6) = 7 is a singleton in the 8th row making (9,6) = 3 a singleton in the 6th column.
Three more singletons: (4,6) = 5 in the 4th row, (6,4) = 6 in the 6th row, and (3,1) = 6 in row 3. But then the singletons dry up:
|
1 34 |
3 7 9 |
1 34 |
1 5 78 |
1 45 89 |
1 4 |
2 |
67 9 |
1 34 6 9 |
|
1234 |
5 |
8 |
12 7 |
12 4 9 |
6 |
34 7 9 |
7 9 |
1 34 9 |
|
6 |
2 7 9 |
12 4 |
3 |
12 4 9 |
12 4 |
4 7 9 |
8 |
5 |
|
23 8 |
1 |
23 |
4 |
7 |
5 |
6 |
2 9 |
2 89 |
|
9 |
4 |
6 |
12 8 |
12 8 |
12 |
5 |
3 |
7 |
|
5 |
2 8 |
7 |
6 |
3 |
9 |
1 |
4 |
2 8 |
|
7 |
6 |
12345 |
12 5 |
12 45 |
8 |
34 9 |
2 5 9 |
234 9 |
|
234 |
23 |
2345 |
9 |
2 456 |
7 |
8 |
1 |
234 6 |
|
12 4 8 |
2 8 |
9 |
12 5 |
12 456 |
3 |
4 7 |
2 567 |
2 4 6 |
Let’s clean up the above array a bit so we can examine it carefully.
|
134 |
379 |
134 |
1578 |
14589 |
14 |
2 |
679 |
13469 |
|
1234 |
5 |
8 |
127 |
1249 |
6 |
3479 |
79 |
1349 |
|
6 |
279 |
124 |
3 |
1249 |
124 |
479 |
8 |
5 |
|
238 |
1 |
23 |
4 |
7 |
5 |
6 |
29 |
289 |
|
9 |
4 |
6 |
128 |
128 |
12 |
5 |
3 |
7 |
|
5 |
28 |
7 |
6 |
3 |
9 |
1 |
4 |
28 |
|
7 |
6 |
12345 |
125 |
1245 |
8 |
349 |
259 |
2349 |
|
234 |
23 |
2345 |
9 |
2456 |
7 |
8 |
1 |
2346 |
|
1248 |
28 |
9 |
125 |
12456 |
3 |
47 |
2567 |
246 |
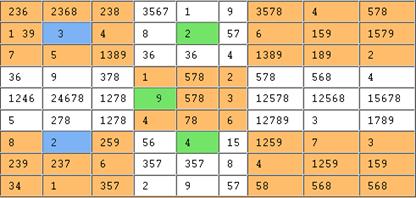
Using exclusive pairs
Look at column 2. In particular, cells (1,2) and (3,2), which contain, respectively, “379” and “279.” Since these are the only two cells in that column that contain either a 7 or a 9, one must be a 7 and the other must be a 9. We don’t know which is which, but we know neither is a 2 nor a 3. Let’s call such a pair an exclusive pair. Then (6,2) = (9,2) = “28” is another exclusive pair in the second column, which means that (8,2) = 3, since it can no longer be a 2. We update the partial solution like so:
|
134 |
79 |
134 |
1578 |
14589 |
14 |
2 |
679 |
13469 |
|
1234 |
5 |
8 |
127 |
1249 |
6 |
3479 |
79 |
1349 |
|
6 |
79 |
124 |
3 |
1249 |
124 |
479 |
8 |
5 |
|
238 |
1 |
23 |
4 |
7 |
5 |
6 |
29 |
289 |
|
9 |
4 |
6 |
128 |
128 |
12 |
5 |
3 |
7 |
|
5 |
28 |
7 |
6 |
3 |
9 |
1 |
4 |
28 |
|
7 |
6 |
1245 |
125 |
1245 |
8 |
349 |
259 |
2349 |
|
24 |
3 |
245 |
9 |
2456 |
7 |
8 |
1 |
246 |
|
1248 |
28 |
9 |
125 |
12456 |
3 |
47 |
2567 |
246 |
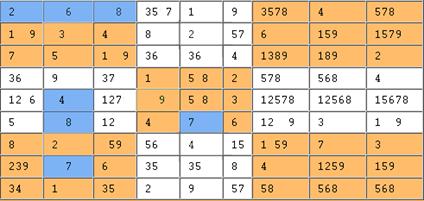
There are no more
exclusive pairs at this point…though, in practice, this takes some close
inspection to ascertain (you need to look at 27 different groupings of 9
cells: 9 columns, 9 rows and 9 clocks.)
So we move onto step 6 in this algorithm:
Guess and check with exclusive triples
The logical next
phase would be the exclusive triple:
three cells in particular group (row, column, block) that contain only three different numerals this would mean none of these three numerals
could occur in another cell of that group.
Column 6 has an exclusive triple, but it is of no immediate use, since
none of the numerals 1, 2 or 4 appear in another cell of that column. By contrast, the first row has (1,1) (1,3)
and (1,6) containing only 1,3 and/or 4, so we can update the partial solution
like so:
|
134 |
79 |
134 |
578 |
589 |
14 |
2 |
679 |
69 |
|
1234 |
5 |
8 |
127 |
1249 |
6 |
3479 |
79 |
1349 |
|
6 |
79 |
124 |
3 |
1249 |
124 |
479 |
8 |
5 |
|
238 |
1 |
23 |
4 |
7 |
5 |
6 |
29 |
289 |
|
9 |
4 |
6 |
128 |
128 |
12 |
5 |
3 |
7 |
|
5 |
28 |
7 |
6 |
3 |
9 |
1 |
4 |
28 |
|
7 |
6 |
1245 |
125 |
1245 |
8 |
349 |
259 |
2349 |
|
24 |
3 |
245 |
9 |
2456 |
7 |
8 |
1 |
246 |
|
1248 |
28 |
9 |
125 |
12456 |
3 |
47 |
2567 |
246 |
This shows that
the upper right block has an exclusive triple: (1,8), (1,9) and (2,8)
containing “679”, so we can update again:
|
134 |
79 |
134 |
578 |
589 |
14 |
2 |
679 |
69 |
|
24 |
5 |
8 |
27 |
249 |
6 |
3 |
79 |
1 |
|
6 |
79 |
12 |
3 |
129 |
12 |
4 |
8 |
5 |
|
238 |
1 |
23 |
4 |
7 |
5 |
6 |
29 |
289 |
|
9 |
4 |
6 |
128 |
128 |
12 |
5 |
3 |
7 |
|
5 |
28 |
7 |
6 |
3 |
9 |
1 |
4 |
28 |
|
7 |
6 |
1245 |
125 |
1245 |
8 |
9 |
25 |
234 |
|
24 |
3 |
245 |
9 |
2456 |
7 |
8 |
1 |
246 |
|
1248 |
28 |
9 |
125 |
12456 |
3 |
7 |
256 |
246 |
This is a big cascade of consequences which can be enumerated in order like
so:
· Eliminating other 6,7,9 numerals in the upper right block means (3,7) = 4
· That means that (2,9) = 1, (2,7) = 3 and (9,7) = 7, so
· (7,7) = 9
·
After updating for these changes we see that there are a number of new exclusive triples, but none of much immediate consequence. In the first row, (1,2), (1,8) and (1,9) are an exclusive triple so we can eliminate 7 and 9 from the other cells in the first row. Also, in the 6th column, (3,6) and (5,6) are an exclusive double so (1,6) = 4 which means the top middle block has an exclusive triple and thus (2,4) = 7, causing (2,8) = 9 and we can solve the upper right block.
Updating the partial solution to reflect these values we have the following:
|
13 |
9 |
13 |
58 |
58 |
4 |
2 |
7 |
6 |
|
24 |
5 |
8 |
7 |
29 |
6 |
3 |
9 |
1 |
|
6 |
7 |
12 |
3 |
129 |
12 |
4 |
8 |
5 |
|
238 |
1 |
23 |
4 |
7 |
5 |
6 |
29 |
289 |
|
9 |
4 |
6 |
128 |
128 |
12 |
5 |
3 |
7 |
|
5 |
28 |
7 |
6 |
3 |
9 |
1 |
4 |
28 |
|
7 |
6 |
1245 |
125 |
1245 |
8 |
9 |
25 |
234 |
|
24 |
3 |
245 |
9 |
2456 |
7 |
8 |
1 |
24 |
|
1248 |
28 |
9 |
125 |
12456 |
3 |
7 |
256 |
24 |
The consequences seem to come quickly and I arrive at this nearly finished solution here. Take a moment to finish it if you can.
|
3 |
9 |
1 |
58 |
58 |
4 |
2 |
7 |
6 |
|
4 |
5 |
8 |
7 |
2 |
6 |
3 |
9 |
1 |
|
6 |
7 |
2 |
3 |
9 |
1 |
4 |
8 |
5 |
|
8 |
1 |
3 |
4 |
7 |
5 |
6 |
2 |
9 |
|
9 |
4 |
6 |
128 |
18 |
12 |
5 |
3 |
7 |
|
5 |
2 |
7 |
6 |
3 |
9 |
1 |
4 |
8 |
|
7 |
6 |
45 |
125 |
145 |
8 |
9 |
5 |
3 |
|
24 |
3 |
45 |
9 |
456 |
7 |
8 |
1 |
24 |
|
1 |
8 |
9 |
25 |
45 |
3 |
7 |
6 |
24 |
Enlightened Guess and Check
If this method using singletons, exclusive doubles and triples don’t lead to a solution (I’d like to see an example of that), then the desperate phase (one hopes) enlightened guess and check. If you have an exclusive double, say, (1,4) = (1,5) = “ 58” above and assume that (1,4) = 5 so (1,5) = 8 and see if the consequences work out or if you arrive at a contradiction. The tricky part is keeping track of what you’ve tried and having some pencil/paper technique for writing it out.
Thanks to Cal State L.A. Mathematics Professor Mike Krebs http://www.calstatela.edu/faculty/gbrookf/pubs/minisudoku.pdf
And etc.












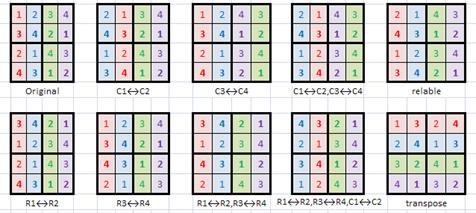
 or
or